如何在 Java 中实现无向环和有向环的检测

一个含有环的无向图如下所示，其中有两个环，分别是 0-2-1-0 和 2-3-4-2：

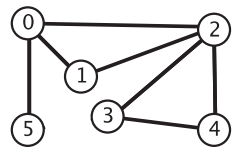
要检测无向图中的环，可以使用深度优先搜索。假设从顶点 0 出发，再走到相邻的顶点 2，接着走到顶点 2 相邻的顶点 1，由于顶点 0 和顶点 1 相邻，并且顶点 0 被标记过了，说明我们饶了一圈，所以无向图中存在环。虽然顶点 2 和顶点 1 相邻，但是并不能说明存在环，因为我们就是从顶点 2 直接走到顶点 1 的，这二者只有边的关系。算法如下所示：

package com.zhiyiyo.graph;  import com.zhiyiyo.collection.stack.LinkStack; import com.zhiyiyo.collection.stack.Stack;  /**  * 无向图中的环  */ public class Cycle {     private boolean[] marked;     private Graph graph;     private boolean hasCycle;      public Cycle(Graph graph) {         this.graph = graph;         marked = new boolean[graph.V()];          for (int v = 0; v < graph.V(); ++v) {             if (!marked[v]) {                 dfs(v);             }         }     }      private void dfs(int s) {         if (hasCycle()) return;          Stack<Integer> vertexes = new LinkStack<>();         vertexes.push(s);         marked展开 = true;          int lastVertex = s;         while (!vertexes.isEmpty()) {             int v = vertexes.pop();              for (int w : graph.adj(v)) {                 if (!marked[w]) {                     marked[w] = true;                     vertexes.push(w);                 } else if (w != lastVertex) {                     hasCycle = true;                     return;                 }             }              lastVertex = v;         }     }      /**      * 图中是否有环      */     public boolean hasCycle() {         return hasCycle;     } }

有向图

有向图的实现方式和上一篇博客《如何在 Java 中实现无向图》 中无向图的实现方式几乎一样，只是在添加边 v-w 时只在顶点 v 的链表上添加顶点 w，而不对顶点 w 的链表进行操作。如果把LinkGraph 中成员变量的访问权限改成protected，只需继承并重写addEdge 方法即可：

package com.zhiyiyo.graph;   public class LinkDigraph extends LinkGraph implements Digraph {      public LinkDigraph(int V) {         super(V);     }      @Override     public void addEdge(int v, int w) {         adj[v].push(w);         E++;     }      @Override     public Digraph reverse() {         Digraph digraph = new LinkDigraph(V());         for (int v = 0; v < V(); ++v) {             for (int w : adj(v)) {                 digraph.addEdge(w, v);             }         }         return digraph;     } }

检测算法

一个含有有向环的有向图如下所示，其中 5-4-3-5 构成了一个环：

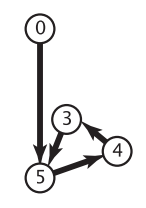
这里使用递归实现的深度优先搜索来检测有向环。假设从顶点 0 开始走，一路经过 5、4、3 这三个顶点，最终又碰到了与顶点 3 相邻的顶点 5，这时候如果知道顶点 5 已经被访问过了，并且递归函数还被压在栈中，就说明深度优先搜索从顶点 5 开始走，又回到了顶点 5，也就是找到了有向环。算法如下所示：

package com.zhiyiyo.graph;  import com.zhiyiyo.collection.stack.LinkStack; import com.zhiyiyo.collection.stack.Stack;  /**  * 有向图中的环  */ public class DirectedCycle {     private boolean[] marked;     private boolean[] onStack;     private int[] edgeTo;     private Graph graph;     private Stack<Integer> cycle;      public DirectedCycle(Digraph graph) {         this.graph = graph;         marked = new boolean[graph.V()];         onStack = new boolean[graph.V()];         edgeTo = new int[graph.V()];          for (int v = 0; v < graph.V(); ++v) {             if (!marked[v]) {                 dfs(v);             }         }     }      private void dfs(int v) {         marked[v] = true;         onStack[v] = true;          for (int w : graph.adj(v)) {             if (hasCycle()) return;             if (!marked[w]) {                 marked[w] = true;                 edgeTo[w] = v;                 dfs(w);             } else if (onStack[w]) {                 cycle = new LinkStack<>();                 cycle.push(w);                 for (int i = v; i != w; i = edgeTo[i]) {                     cycle.push(i);                 }                 cycle.push(w);             }         }          onStack[v] = false;     }      /**      * 图中是否有环      */     public boolean hasCycle() {         return cycle != null;     }      /**      * 图中的一个环      */     public Iterable<Integer> cycle() {         return cycle;     } }